pomocy Paweł: Czesć mam ogromna prozbe grozi mi jedynka z matmy musze zrobic kilka zadan aby dostac pozytywna ocene mam tutaj taki przyklad i byłbym wdzieczny gdyby ktos mi go pomogł zrobic wytłumaczyc ? Zadanie a) pole szesciokata formenego jest rowne 12√3 cm².oblicz promień okregu opisanego na tym szesciokacie i promien okregu w niego wpisanego. b) promien okregu wpisanego w szesciokat foremny jest rowny 1 cm .oblicz obwod i pole tego szesciokata to takie przykladowe zadania prosze o pomoc a reszte sprobuje rozwiazac sam

Paweł: pomoże mi ktos

ICSP: 1. a = R

	a√3
		= r
	2

R − promień kręgu opisanego r − promień okręgu wpisanego a − bok P − pole sześciokąta foremnego

	3
P =		a2√3. Z tego wyznaczasz a i później wstawiasz do wyżej podanych wzorków.
	2

ICSP: Obw = 6a. Teraz masz już wszystkie wzorki. Zadania to tylko operowanie na tych wzorkach.

Paweł: jak to przekształcie?

Paweł: aaa juz powoli cos rozumiem ale nie do konca

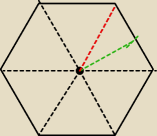Grześ: Pole sześciokąta złożone jest z pola 6 trójkątów równobocznych o boku a Kolorem zielonym zaznaczony jest promień okręgu wpisanego, a czerwonym opisanego. Czyli pole jednego trójkąta wynosi:

	12√3
PΔ=		=2√3
	6

Teraz ze wzoru na pole trójkąta liczysz "a"

	a2√3
PΔ=
	4

Po wyliczeniu "a" masz taką zależność: a=r(okrąg wpisany) h=r(okrąg opisany) Dasz radę

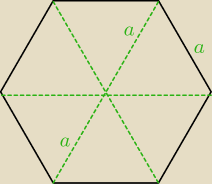PanCogito: Sześciokąt foremny to sześć trójkątów równobocznych, każdy o boku a. Prómień tego okręgu ma długość r = 2a.

	a2√3
P(sześciokąta) = 6*Ptrójkąta o boku a ⇒ 12√3 = 6*		⇒ a = 2√2
	4

r = 2a ⇒ r=4√2

Paweł: czyli : 3 P= −−− a²√3 2 r=4√2 a=2√2 a jak obliczyc R promien okregu opisanego i co z drugim zadaniem

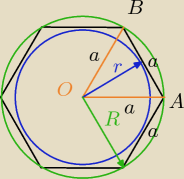dero2005: zad a) dane : pole sześciokąta foremnego równa się 12√3 cm² pole sześciokąta foremnego sklada się z pól sześciu trójkątów równobocznych AOB czyli pole jednego trójkata jest równe

	12√3
P =		= 2√3
	6

	a2√3
Pole trójkąta równobocznego obliczamy ze wzoru P=		gdzie a = bok trójkąta = R =
	4

promień okręgu opisanego na sześciokącie

	4P		4*2√3
przekształcając wzór otrzymujemy a2 =		=		= 8
	√3		√3

a = √8 = 2√2 cm = R → promień okręgu opisanego wysokość trójkąta równobocznego AOB = h = r → promień okręgu wpisanego wysokość trójkąta równobocznego obliczamy ze wzoru

	a√3		2√2*√3
h =		=		= √6 cm = r → promień okręgu wpisanego
	2		2

Paweł: dzieki daro juz zaczaiłem troche tylko z tym drugim mam problem

dero2005: dane r = 1 r = 1 − promień okręgu wpisanego jest równy wysokości trójkąta równobocznego OAB o boku a wzór na wysokość w trójkącie równobocznym wygląda tak

	a√3
h =
	2

przekształcając wzór obliczamy a a = ²₃√3h = ²₃√3*1 Obwód sześciokąta wynosi O = 6a = 6*²₃√3 = 4√3 Pole sześciokąta foremnego wynosi P_⬡ = ³₂a²√3 = (²₃)²*³₂√3 = 2√3 cm

Paweł: ooo dzieki wielkie teraz sprobuje rozwiazac reszte sa bardzo podobne wiec nie bedzie chyba problemu